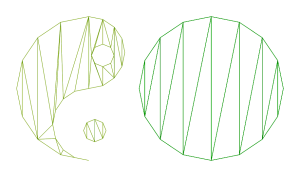In this second part of the tutorial I will be covering drawing without using direct mode as well as drawing complex polygons. If you don’t know how to set up a basic OpenGL application in Java, please read Part 1.
Drawing Using Vertex Arrays and Buffers
Vertex Arrays
One Color Per Array
In Part 1, I rendered a triangle on the screen using direct mode. Opponents of this technique will tell you that it can be quite slow compared to other rendering methods. The main reason for this is that the computer makes one function call per vertex. This is a problem when rendering complicated images because the function calls are expensive time-wise, as they have to push data to the GPU separately. The solution to this problem is to put all the data into an array (as we have already done) and then upload the array to the GPU all at once.
float[] triangle = {
128, 128, 0,
256, 128, 0,
192, 256, 0
};
FloatBuffer vertices = BufferUtils.createFloatBuffer(triangle.length);
vertices.put(triangle);
vertices.flip();
The above code goes before the rendering loop begins. The bottom three lines would not be present in the C equivalent of this code and warrant some explanation. In C the code would look like this:
//this is C code; don't try to use it in a Java project
GLfloat triangle[] = {
128, 128, 0,
256, 128, 0,
192, 256, 0
};
At this point you would pass the array directly to the glVertexPointer() function and OpenGL would draw whatever was in the array. Unfortunately things cannot be that smooth in Java because Java’s arrays are not simple pointers to memory locations as are C’s. The workaround for this chosen by the LWJGL developers was to use Java’s Buffer and associated subclasses backed by native arrays. They provide us with special methods for allocating this memory in the BufferUtils class. Thus we must first allocate the memory, then insert the data, and finally call flip() to set the ByteBuffer pointer back to the beginning of the array. For more on the hows and whys of Java’s Buffer classes see the Java API Documentation.
After putting the vertex data into the memory, you can tell the graphics card to render it from your rendering loop as follows.
glEnableClientState(GL_VERTEX_ARRAY); glVertexPointer(3, 0, vertices); glDrawArrays(GL_TRIANGLES, 0, triangle.length / 3); glDisableClientState(GL_VERTEX_ARRAY);
Notice that you must divide the length of the array by three when passing it to the glDrawArrays() function. This is necessary because it is expecting to receive the number of vertices, not the number of individual Cartesian coordinates.
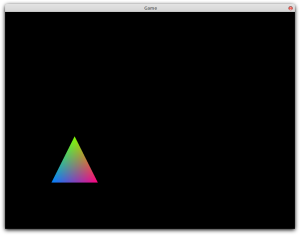
At this point your program should render exactly the same triangle as it did when using direct mode. See Appendix A for the entire code of the vertex array example.
One Color Per Vertex
In Part 1 I demonstrated how to define the colors of your vertices as part of an array. It is also possible to do this when using vertex arrays. First you have to make a separate buffer for the colors (it is possible to put the colors in the same array with the vertices when using Vertex Buffers, covered in the next section under Interleaved VBO).
float[] colors = {
0, 0.5f, 1,
1, 0, 0.5f,
0.5f, 1, 0
};
FloatBuffer verticeColors = BufferUtils.createFloatBuffer(colors.length);
verticeColors.put(colors);
verticeColors.flip();
Next you would change the drawing code to enable color arrays, and include a pointer to the color array.
glEnableClientState(GL_VERTEX_ARRAY); glEnableClientState(GL_COLOR_ARRAY); glVertexPointer(3, 0, vertices); glColorPointer(3, 0, verticeColors); glDrawArrays(GL_TRIANGLES, 0, triangle.length / 3); glDisableClientState(GL_COLOR_ARRAY); glDisableClientState(GL_VERTEX_ARRAY);
After doing so your program should render a pretty multicolored triangle.
Vertex Buffers
One Color Per Polygon / Vertex Colors in Separate Array
Vertex buffer objects (VBOs), not to be confused with Java’s Buffer classes, are similar to vertex arrays. The only difference is that the vertex data is copied into the graphics memory once and stays there, rather than being re-uploaded every frame. Vertex buffers were introduced in OpenGL 1.5, so you need to import the corresponding functions and constants if you have not already (see Part 1 section “Including LWJGL in your project” for how to do this).
In order to upload data directly to the GPU memory you first need to generate a pointer by which to access your data. This pointer is an integer number that corresponds to an address in the graphics memory.
int verticeHandle = glGenBuffers();
Then you upload your FloatBuffer to the location specified by the pointer.
glBindBuffer(GL_ARRAY_BUFFER, verticeHandle); glBufferData(GL_ARRAY_BUFFER, vertices, GL_STATIC_DRAW);
If you are using colors you would do the same thing for your color array. The glBindBuffer() function tells OpenGL to prepare the buffer in question for manipulation (in this case that would be the buffer represented by “verticeHandle”). The glBufferData() function loads data into the currently bound buffer. After loading the data, you should tell the graphics card to use your newly filled buffer as a source for vertex information.
glVertexPointer(3, GL_FLOAT, 0, 0);
The glVertexPointer() function establishes a pointer to the current buffer as the vertex location. You may do the same thing for colors simply by changing the function name to glColorPointer().
Now you are ready to render the triangle from within the rendering loop. The same function is used as for rendering vertex arrays. This time you don’t need to call glVertexPointer() inside the rendering loop, though.
glDrawArrays(GL_TRIANGLES, 0, triangle.length / 3);
After making these changes your output should once again be identical to previous iterations of your program. If it is not, compare your code with that in Appendix B.
One Color Per Vertex (Interleaved VBO)
As I mentioned in the section on vertex arrays, when using vertex buffers it is possible to store your vertices and colors in one array if desired. Whether or not there is a performance gain in doing so is questionable, so it really comes down to what’s convenient for you. The implementation is relatively simple. First add the extra color information to your vertex array.
float[] triangle = {
128, 128, 0, 0, 0.5f, 1,
256, 128, 0, 1, 0, 0.5f,
192, 256, 0, 0.5f, 1, 0
};
Next modify your pointer definition to account for the wider array.
glVertexPointer(3, GL_FLOAT, 6 << 2, 0); glColorPointer(3, GL_FLOAT, 6 << 2, 3 << 2);
Notice that you are now using the third and fourth parameters of glVertexPointer(). The third parameter is called “stride,” and it represents the size of each vertex in the array. When it is set to 0, it assumes that the array is “tightly packed,” meaning that there is no space in between the vertices. In this case writing 0 would have been equivalent to writing 3 << 2. The stride is defined in bytes, which is why the “<< 2” must be included. Since there are an extra three floats at the end of each vertex, representing color, you have to use 6 << 2 (24 bytes) as your stride. The fourth parameter is the offset from the beginning of the vertex entry at which the data is located. The vertex itself is at the beginning and therefore has an offset of 0. The color information comes right afterward, so it has an offset of 3 floats, or 12 bytes (3 << 2). After making these changes and enabling color arrays (glEnableClientState(GL_COLOR_ARRAY), and corresponding disable call), you should see a colorful triangle identical to the one in previous vertex color examples.
Drawing Complex Polygons
While there is a drawing mode called GL_POLYGON, it doesn’t work on concave or self-intersecting polygons. The graphics card and OpenGL by extension are actually capable of efficiently drawing only triangles. Therefore, if you want to draw an interesting polygon you must first divide it up into triangles. This process is called tessellation. LWJGL ships with a Java implementation of the GLU Tessellator (they spell it “tesselator” for some reason I cannot fathom) which is more than adequate for our purposes.
Note: The meshes produced by the GLU Tessellator can contain some very long, thin triangles that could be deemed inefficient. If you think the output is unsuitable for your purposes there are alternative tessellation options. I recommend looking into Delaunay triangulation algorithms.
Tessellating in Direct Mode
By default, the tessellator makes direct mode function calls to draw the triangles it produces. Since it requires little modification to do this, it’s easiest to learn it this way.
Let’s start by defining the shape we’re going to draw. It consists of several polygons, some of which are convex and have holes. It is defined in a three-dimensional array of doubles with a hierarchy of Polygon > Contour > Vertices.
double[][][] complicatedShape = {
{
{
620.15417, 300.00001, 0, 0, 0.66, 0,
602.85338, 214.30606999999998, 0, 0, 0.66, 0,
555.67249, 144.32745999999997, 0, 0, 0.66, 0,
485.69398, 97.14663999999999, 0, 0, 0.66, 0,
400, 79.84582, 0, 0, 0.66, 0,
314.30601, 97.14663999999999, 0, 0, 0.66, 0,
244.32752, 144.32745999999997, 0, 0, 0.66, 0,
197.14662, 214.30606999999998, 0, 0, 0.66, 0,
179.84583, 300.00001, 0, 0, 0.66, 0,
197.14662, 385.69395, 0, 0, 0.66, 0,
244.32752, 455.67251, 0, 0, 0.66, 0,
314.30601, 502.853335, 0, 0, 0.66, 0,
400, 520.154145, 0, 0, 0.66, 0,
485.69398, 502.853335, 0, 0, 0.66, 0,
555.67249, 455.67251, 0, 0, 0.66, 0,
602.85338, 385.69395, 0, 0, 0.66, 0
}
},
{
{
399.96981, 520.154415, 0, 0.66, 0.87, 0.53,
314.31022, 502.84844499999997, 0, 0.66, 0.87, 0.53,
244.33872000000002, 455.66152, 0, 0.66, 0.87, 0.53,
197.15180000000004, 385.69002, 0, 0.66, 0.87, 0.53,
179.84583000000003, 300.03043, 0, 0.66, 0.87, 0.53,
197.15180000000004, 214.36131, 0, 0.66, 0.87, 0.53,
244.33872000000002, 144.36892, 0, 0.66, 0.87, 0.53,
314.31022, 97.16106000000002, 0, 0.66, 0.87, 0.53,
399.96981, 79.84559000000002, 0, 0.66, 0.87, 0.53,
357.14002, 88.49858, 0, 0.66, 0.87, 0.53,
322.15427, 112.09205000000003, 0, 0.66, 0.87, 0.53,
298.5608, 147.07779000000005, 0, 0.66, 0.87, 0.53,
289.90781999999996, 189.90759000000003, 0, 0.66, 0.87, 0.53,
298.5608, 232.74691, 0, 0.66, 0.87, 0.53,
322.15427, 267.75356, 0, 0.66, 0.87, 0.53,
357.14002, 291.36794, 0, 0.66, 0.87, 0.53,
399.96981, 300.03042999999997, 0, 0.66, 0.87, 0.53,
442.79961, 308.68341, 0, 0.66, 0.87, 0.53,
477.78535, 332.27689, 0, 0.66, 0.87, 0.53,
501.37883, 367.26262999999994, 0, 0.66, 0.87, 0.53,
510.03181, 410.09241999999995, 0, 0.66, 0.87, 0.53,
501.37883, 452.92222, 0, 0.66, 0.87, 0.53,
477.78535, 487.90797999999995, 0, 0.66, 0.87, 0.53,
442.79961, 511.501435, 0, 0.66, 0.87, 0.53
},
{
442.79961, 435.81479, 0, 0.66, 0.87, 0.53,
467.13788, 425.74728, 0, 0.66, 0.87, 0.53,
477.23582, 401.43944, 0, 0.66, 0.87, 0.53,
467.13788, 377.10117, 0, 0.66, 0.87, 0.53,
442.79961, 367.00324, 0, 0.66, 0.87, 0.53,
418.49177, 377.10117, 0, 0.66, 0.87, 0.53,
408.42425, 401.43944, 0, 0.66, 0.87, 0.53,
418.49177, 425.74728, 0, 0.66, 0.87, 0.53
},
{
418.49177, 205.62329999999997, 0, 0.66, 0.87, 0.53,
394.18129999999996, 195.52799999999996, 0, 0.66, 0.87, 0.53,
384.11641, 171.1871, 0, 0.66, 0.87, 0.53,
394.18129999999996, 146.87662999999998, 0, 0.66, 0.87, 0.53,
418.49177, 136.81174, 0, 0.66, 0.87, 0.53,
442.83266999999995, 146.87662999999998, 0, 0.66, 0.87, 0.53,
452.92796999999996, 171.1871, 0, 0.66, 0.87, 0.53,
442.83266999999995, 195.52799999999996, 0, 0.66, 0.87, 0.53
}
}
};
We could attempt to render this using the GL_POLYGON mode as follows.
for (double[][] polygon : complicatedShape) {
glBegin(GL_POLYGON);
for (double[] contour : polygon) {
for (int i = 0; i < contour.length - 5; i += 6) {
glColor3f((float) contour[i + 3], (float) contour[i + 4], (float) contour[i + 5]);
glVertex3f((float) contour[i], (float) contour[i + 1], (float) contour[i + 2]);
}
}
glEnd();
}
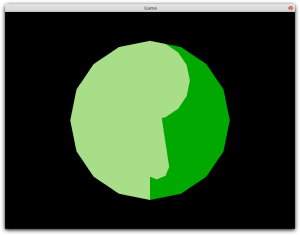
Unfortunately, because of the aforementioned limitations in OpenGL this won’t work very well. To be precise it will look like this:
I want what it will look like when we’re finished to be a surprise, so I won’t show you what it’s supposed to look like yet (if you’re really curious you can scroll down to see).
The tessellator is included as part of lwjgl_util.jar, instructions on including that in your project are in Part 1. In order to use the tools in the GLU package, you must import the associated functions in the same manner as for the regular OpenGL functions.
import static org.lwjgl.util.glu.GLU.*;
Now you can create a new tessellator using the gluNewTess() function.
GLUtessellator tessellator = gluNewTess();
GLUtessellatorCallback callback = new GLUtessellatorCallbackAdapter() {
@Override
public void begin(int type) {
glBegin(type);
}
@Override
public void end() {
glEnd();
}
@Override
public void vertex(Object data) {
double[] vertexData = (double[]) data;
glColor3d(vertexData[3], vertexData[4], vertexData[5]);
glVertex3d(vertexData[0], vertexData[1], vertexData[2]);
}
@Override
public void combine(double[] coords, Object[] data, float[] weight, Object[] outData) {
double[] combined = {coords[0], coords[1], coords[2], 0, 0, 0};
for (int i = 0; i < data.length; i++) {
double[] vertex = (double[]) data[i];
combined[3] += weight[i] * vertex[3];
combined[4] += weight[i] * vertex[4];
combined[5] += weight[i] * vertex[5];
}
outData[0] = combined;
}
};
tessellator.gluTessCallback(GLU_TESS_BEGIN, callback);
tessellator.gluTessCallback(GLU_TESS_END, callback);
tessellator.gluTessCallback(GLU_TESS_VERTEX, callback);
tessellator.gluTessCallback(GLU_TESS_COMBINE, callback);
The tessellator uses an event-driven model that will be familiar to anybody who has programmed in JavaScript before. The tessellator triggers events whenever it has data to send back and it is up to a callback object that you define to decide what to do with that data. In this case we registered a callback for GLU_TESS_BEGIN, GLU_TESS_END, GLU_TESS_VERTEX and GLU_TESS_COMBINE. GLU_TESS_BEGIN is called at the beginning of a primitive, GLU_TESS_VERTEX is called when a new vertex is available, and GLU_TESS_END is called when the primitive is fully defined. The “type” parameter that is passed to the begin() method corresponds to the type of primitive that the tessellator is defining. By default, the tessellator uses GL_TRIANGLES, GL_TRIANGLE_STRIP and GL_TRIANGLE_FAN as its primitive types. For an explanation of what triangle strips and fans are, see this answer on StackOverflow.
The combine() method is called when the tessellator needs to combine two vertices. It is capable of combining the coordinates of the vertices by itself, however it cannot combine the arbitrary data (in this case color) that we might have passed with each vertex. The tessellator will call the combine() method with the coordinates of the combined vertices, with an array consisting of the arbitrary data we have passed it, with an array of weights for each vertex, and finally with an array we are to put the combined data into. The last parameter is essentially what is known as a pointer in C; it is passed as an array of length 1 because Java doesn’t directly support passing object references to methods.
Once the tessellator has been created, and the callback methods defined, you can start feeding the data to the tessellator. You should do this inside of the rendering loop, so that your drawing functions get called in every frame.
for (double[][] polygon : complicatedShape) {
tessellator.gluTessBeginPolygon(null);
for (double[] contour : polygon) {
tessellator.gluTessBeginContour();
for (int i = 0; i < contour.length - 5; i += 6) {
double[] vertexData = {
contour[i], contour[i + 1], contour[i + 2],
contour[i + 3], contour[i + 4], contour[i + 5]
};
tessellator.gluTessVertex(vertexData, 0, vertexData);
}
tessellator.gluTessEndContour();
}
tessellator.gluTessEndPolygon();
}
Note: There are many tutorials that advise you to call gluDeleteTess() when you’ve finished with the tessellator, so that the tessellator’s memory might be freed. This is sound when using the C implementation of the tessellator. However, the LWJGL implementation is written entirely in Java and therefore has no control over the memory it uses. If you take a look in the LWJGL source code at GLUtessellatorImpl.java, you will see that the gluDeleteTess() method merely throws an error if the tessellator is not in a state to be deleted, it does not delete anything. So, while calling gluDeleteTess() is harmless, it doesn’t do anything of great importance and may be safely omitted.
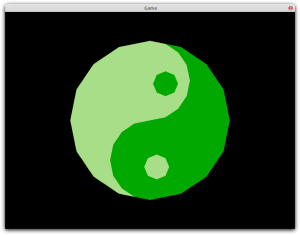
It should now be possible to run your program and see a beautifully rendered shape. If it does not look like the screenshot below, please compare your code against that in Appendix C.
This works because the tessellator has translated the polygons you fed it into triangles as seen in the illustration below.
Tessellating into a Vertex Buffer
As you can imagine, tessellating your polygons in the render loop is horribly inefficient and would not be viable in situations involving hundreds of thousands of shapes. The solution to this problem is to tessellate ahead of time, and save the results into a vertex buffer. In order to accomplish this we have to start by creating a data structure in which to store the vertices. I have chosen to use an ArrayList for this purpose, mainly because I don’t want to bother calculating ahead of time how many vertices I’m going to end up with.
final List allTriangles = new ArrayList<>();
Note that I’m using Java 7 generic syntax in the examples; change the constructor accordingly for older versions. Since this time around you will be drawing the entire shape with one call to glDrawArrays(), you can no longer use different drawing modes. The C version of the GLU Tessellator allows you to pass it a flag that will cause it to only return GL_TRIANGLES, which would be perfect for this use case. Unfortunately the Java version doesn’t work properly when instructed to return only triangles (it leaves out about half of the polygons). To work around this, my solution was to write functions that convert the other two drawing modes to triangles. If somebody figures out or already has a better solution, I would love to hear about it.
public List stripToTriangles(List strip) {
List triangles = new ArrayList<>();
for (int i = 0; i < strip.size() - 12; i += 6) {
triangles.addAll(strip.subList(i, i + 18));
}
return triangles;
}
public List fanToTriangles(List fan) {
List centralVertex = fan.subList(0, 6),
triangles = new ArrayList<>();
for (int i = 6; i < fan.size() - 6; i += 6) {
triangles.addAll(centralVertex);
triangles.addAll(fan.subList(i, i + 12));
}
return triangles;
}
You are now ready to start modifying the tessellator callback to store vertices instead of drawing them.
int type;
List vertices = new ArrayList<>();
@Override
public void begin(int type) {
this.type = type;
vertices.clear();
}
@Override
public void end() {
switch (type) {
case GL_TRIANGLES:
break;
case GL_TRIANGLE_FAN:
this.vertices = fanToTriangles(vertices);
break;
case GL_TRIANGLE_STRIP:
this.vertices = stripToTriangles(vertices);
break;
}
allTriangles.addAll(vertices);
}
@Override
public void vertex(Object data) {
double[] vertexData = (double[]) data;
for (double d : vertexData) vertices.add(d);
}
First you should add two fields to the callback: one to store the type until we need it, and one to store the vertices until we have a complete list. Next, change the begin() method so that it stores the type and clears the vertex list. Change the end() method so that it converts instances of GL_TRIANGLE_FAN and GL_TRIANGLE_STRIP into triangles, using the functions I provided earlier. Then add all the vertices stored so far to the main vertex container. Finally, change the vertex() method so that it adds each vertex to your vertex list. The combine() method is the same as it was before, so I haven’t included it here.
The next step is to move the tessellation loop out of the rendering loop. Apart from running only once, it has not changed from the direct mode tessellation example. Now that all your vertices have been tessellated and stored in your allTriangles list you have to copy them into a buffer to send them to OpenGL.
FloatBuffer vertices = BufferUtils.createFloatBuffer(allTriangles.size()); for (double d : allTriangles) vertices.put((float) d); vertices.flip(); int verticeHandle = glGenBuffers(); glBindBuffer(GL_ARRAY_BUFFER, verticeHandle); glBufferData(GL_ARRAY_BUFFER, vertices, GL_STATIC_DRAW); glVertexPointer(3, GL_FLOAT, 6 << 2, 0); glColorPointer(3, GL_FLOAT, 6 << 2, 3 << 2);
The only thing left to do is to change the rendering loop to draw your new interleaved buffer.
glEnableClientState(GL_VERTEX_ARRAY);
glEnableClientState(GL_COLOR_ARRAY);
while (!Display.isCloseRequested()) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glDrawArrays(GL_TRIANGLES, 0, allTriangles.size() / 6);
Display.update();
Display.sync(60);
}
glDisableClientState(GL_COLOR_ARRAY);
glDisableClientState(GL_VERTEX_ARRAY);
You should now be able to run your program and see exactly what you saw when using tessellation with direct mode. If you see a green mess, or nothing at all, it is once again time to check your code, this time against Appendix D.
Closure
Congratulations, you got through Act II! In the most-likely forthcoming Part 3 I will go into how to store indices instead of vertices when tessellating, and maybe finally cover listening on input devices as well. Just as last time, please feel free to contact me with feedback or suggestions.
Appendix A: Complete Code of Vertex Array Example
import static org.lwjgl.opengl.GL11.*;
import java.nio.FloatBuffer;
import org.lwjgl.BufferUtils;
import org.lwjgl.LWJGLException;
import org.lwjgl.opengl.Display;
import org.lwjgl.opengl.DisplayMode;
import org.lwjgl.opengl.PixelFormat;
public class OpenGL2dDemo {
public static void main(String[] argv) {
new OpenGL2dDemo().start();
}
public void start() {
try {
Display.setDisplayMode(new DisplayMode(800, 600));
Display.create(new PixelFormat(0, 8, 0, 0));
} catch (LWJGLException e) {
e.printStackTrace();
System.exit(1);
}
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0, 800, 0, 600, 1, -1);
glMatrixMode(GL_MODELVIEW);
float[] triangle = {
128, 128, 0,
256, 128, 0,
192, 256, 0
};
FloatBuffer vertices = BufferUtils.createFloatBuffer(triangle.length);
vertices.put(triangle);
vertices.flip();
while (!Display.isCloseRequested()) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glColor3f(0, 0.5f, 1);
glEnableClientState(GL_VERTEX_ARRAY);
glVertexPointer(3, 0, vertices);
glDrawArrays(GL_TRIANGLES, 0, triangle.length / 3);
glDisableClientState(GL_VERTEX_ARRAY);
Display.update();
Display.sync(60);
}
}
}
Appendix B: Complete Code of Vertex Buffer Example
import static org.lwjgl.opengl.GL11.*;
import static org.lwjgl.opengl.GL15.*;
import java.nio.FloatBuffer;
import org.lwjgl.BufferUtils;
import org.lwjgl.LWJGLException;
import org.lwjgl.opengl.Display;
import org.lwjgl.opengl.DisplayMode;
import org.lwjgl.opengl.PixelFormat;
public class OpenGL2dDemo {
public static void main(String[] argv) {
new OpenGL2dDemo().start();
}
public void start() {
try {
Display.setDisplayMode(new DisplayMode(800, 600));
Display.create(new PixelFormat(0, 8, 0, 0));
} catch (LWJGLException e) {
e.printStackTrace();
System.exit(1);
}
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0, 800, 0, 600, 1, -1);
glMatrixMode(GL_MODELVIEW);
float[] triangle = {
128, 128, 0,
256, 128, 0,
192, 256, 0
};
FloatBuffer vertices = BufferUtils.createFloatBuffer(triangle.length);
vertices.put(triangle);
vertices.flip();
int verticeHandle = glGenBuffers();
glBindBuffer(GL_ARRAY_BUFFER, verticeHandle);
glBufferData(GL_ARRAY_BUFFER, vertices, GL_STATIC_DRAW);
glVertexPointer(3, GL_FLOAT, 0, 0);
while (!Display.isCloseRequested()) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glColor3f(0, 0.5f, 1);
glEnableClientState(GL_VERTEX_ARRAY);
glDrawArrays(GL_TRIANGLES, 0, triangle.length / 3);
glDisableClientState(GL_VERTEX_ARRAY);
Display.update();
Display.sync(60);
}
}
}
Appendix C: Complete Code of Direct Mode Tessellation Example
import static org.lwjgl.opengl.GL11.*;
import static org.lwjgl.util.glu.GLU.*;
import org.lwjgl.LWJGLException;
import org.lwjgl.opengl.Display;
import org.lwjgl.opengl.DisplayMode;
import org.lwjgl.opengl.PixelFormat;
import org.lwjgl.util.glu.GLUtessellator;
import org.lwjgl.util.glu.GLUtessellatorCallback;
import org.lwjgl.util.glu.GLUtessellatorCallbackAdapter;
public class OpenGL2dDemo {
public static void main(String[] argv) {
new OpenGL2dDemo().start();
}
public void start() {
try {
Display.setDisplayMode(new DisplayMode(800, 600));
Display.create(new PixelFormat(0, 8, 0, 0));
} catch (LWJGLException e) {
e.printStackTrace();
System.exit(1);
}
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0, 800, 0, 600, 1, -1);
glMatrixMode(GL_MODELVIEW);
double[][][] complicatedShape = {
{
{
620.15417, 300.00001, 0, 0, 0.66, 0,
602.85338, 214.30606999999998, 0, 0, 0.66, 0,
555.67249, 144.32745999999997, 0, 0, 0.66, 0,
485.69398, 97.14663999999999, 0, 0, 0.66, 0,
400, 79.84582, 0, 0, 0.66, 0,
314.30601, 97.14663999999999, 0, 0, 0.66, 0,
244.32752, 144.32745999999997, 0, 0, 0.66, 0,
197.14662, 214.30606999999998, 0, 0, 0.66, 0,
179.84583, 300.00001, 0, 0, 0.66, 0,
197.14662, 385.69395, 0, 0, 0.66, 0,
244.32752, 455.67251, 0, 0, 0.66, 0,
314.30601, 502.853335, 0, 0, 0.66, 0,
400, 520.154145, 0, 0, 0.66, 0,
485.69398, 502.853335, 0, 0, 0.66, 0,
555.67249, 455.67251, 0, 0, 0.66, 0,
602.85338, 385.69395, 0, 0, 0.66, 0
}
},
{
{
399.96981, 520.154415, 0, 0.66, 0.87, 0.53,
314.31022, 502.84844499999997, 0, 0.66, 0.87, 0.53,
244.33872000000002, 455.66152, 0, 0.66, 0.87, 0.53,
197.15180000000004, 385.69002, 0, 0.66, 0.87, 0.53,
179.84583000000003, 300.03043, 0, 0.66, 0.87, 0.53,
197.15180000000004, 214.36131, 0, 0.66, 0.87, 0.53,
244.33872000000002, 144.36892, 0, 0.66, 0.87, 0.53,
314.31022, 97.16106000000002, 0, 0.66, 0.87, 0.53,
399.96981, 79.84559000000002, 0, 0.66, 0.87, 0.53,
357.14002, 88.49858, 0, 0.66, 0.87, 0.53,
322.15427, 112.09205000000003, 0, 0.66, 0.87, 0.53,
298.5608, 147.07779000000005, 0, 0.66, 0.87, 0.53,
289.90781999999996, 189.90759000000003, 0, 0.66, 0.87, 0.53,
298.5608, 232.74691, 0, 0.66, 0.87, 0.53,
322.15427, 267.75356, 0, 0.66, 0.87, 0.53,
357.14002, 291.36794, 0, 0.66, 0.87, 0.53,
399.96981, 300.03042999999997, 0, 0.66, 0.87, 0.53,
442.79961, 308.68341, 0, 0.66, 0.87, 0.53,
477.78535, 332.27689, 0, 0.66, 0.87, 0.53,
501.37883, 367.26262999999994, 0, 0.66, 0.87, 0.53,
510.03181, 410.09241999999995, 0, 0.66, 0.87, 0.53,
501.37883, 452.92222, 0, 0.66, 0.87, 0.53,
477.78535, 487.90797999999995, 0, 0.66, 0.87, 0.53,
442.79961, 511.501435, 0, 0.66, 0.87, 0.53
},
{
442.79961, 435.81479, 0, 0.66, 0.87, 0.53,
467.13788, 425.74728, 0, 0.66, 0.87, 0.53,
477.23582, 401.43944, 0, 0.66, 0.87, 0.53,
467.13788, 377.10117, 0, 0.66, 0.87, 0.53,
442.79961, 367.00324, 0, 0.66, 0.87, 0.53,
418.49177, 377.10117, 0, 0.66, 0.87, 0.53,
408.42425, 401.43944, 0, 0.66, 0.87, 0.53,
418.49177, 425.74728, 0, 0.66, 0.87, 0.53
},
{
418.49177, 205.62329999999997, 0, 0.66, 0.87, 0.53,
394.18129999999996, 195.52799999999996, 0, 0.66, 0.87, 0.53,
384.11641, 171.1871, 0, 0.66, 0.87, 0.53,
394.18129999999996, 146.87662999999998, 0, 0.66, 0.87, 0.53,
418.49177, 136.81174, 0, 0.66, 0.87, 0.53,
442.83266999999995, 146.87662999999998, 0, 0.66, 0.87, 0.53,
452.92796999999996, 171.1871, 0, 0.66, 0.87, 0.53,
442.83266999999995, 195.52799999999996, 0, 0.66, 0.87, 0.53
}
}
};
GLUtessellator tessellator = gluNewTess();
GLUtessellatorCallback callback = new GLUtessellatorCallbackAdapter() {
@Override
public void begin(int type) {
glBegin(type);
}
@Override
public void end() {
glEnd();
}
@Override
public void vertex(Object data) {
double[] vertexData = (double[]) data;
glColor3d(vertexData[3], vertexData[4], vertexData[5]);
glVertex3d(vertexData[0], vertexData[1], vertexData[2]);
}
@Override
public void combine(double[] coords, Object[] data, float[] weight, Object[] outData) {
double[] combined = {coords[0], coords[1], coords[2], 0, 0, 0};
for (int i = 0; i < data.length; i++) {
double[] vertex = (double[]) data[i];
combined[3] += weight[i] * vertex[3];
combined[4] += weight[i] * vertex[4];
combined[5] += weight[i] * vertex[5];
}
outData[0] = combined;
}
};
tessellator.gluTessCallback(GLU_TESS_BEGIN, callback);
tessellator.gluTessCallback(GLU_TESS_END, callback);
tessellator.gluTessCallback(GLU_TESS_VERTEX, callback);
tessellator.gluTessCallback(GLU_TESS_COMBINE, callback);
while (!Display.isCloseRequested()) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glColor3f(0, 0.5f, 1);
for (double[][] polygon : complicatedShape) {
tessellator.gluTessBeginPolygon(null);
for (double[] contour : polygon) {
tessellator.gluTessBeginContour();
for (int i = 0; i < contour.length - 5; i += 6) {
double[] vertexData = {
contour[i], contour[i + 1], contour[i + 2],
contour[i + 3], contour[i + 4], contour[i + 5]
};
tessellator.gluTessVertex(vertexData, 0, vertexData);
}
tessellator.gluTessEndContour();
}
tessellator.gluTessEndPolygon();
}
Display.update();
Display.sync(60);
}
}
}
Appendix D: Complete Code of Buffered Tessellation Example
import static org.lwjgl.opengl.GL11.*;
import static org.lwjgl.opengl.GL15.*;
import static org.lwjgl.util.glu.GLU.*;
import java.nio.FloatBuffer;
import java.util.ArrayList;
import java.util.List;
import org.lwjgl.BufferUtils;
import org.lwjgl.LWJGLException;
import org.lwjgl.opengl.Display;
import org.lwjgl.opengl.DisplayMode;
import org.lwjgl.opengl.PixelFormat;
import org.lwjgl.util.glu.GLUtessellator;
import org.lwjgl.util.glu.GLUtessellatorCallback;
import org.lwjgl.util.glu.GLUtessellatorCallbackAdapter;
public class OpenGL2dDemo {
public static void main(String[] argv) {
new OpenGL2dDemo().start();
}
public void start() {
try {
Display.setDisplayMode(new DisplayMode(800, 600));
Display.create(new PixelFormat(0, 8, 0, 0));
} catch (LWJGLException e) {
e.printStackTrace();
System.exit(1);
}
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
glOrtho(0, 800, 0, 600, 1, -1);
glMatrixMode(GL_MODELVIEW);
double[][][] complicatedShape = {
{
{
620.15417, 300.00001, 0, 0, 0.66, 0,
602.85338, 214.30606999999998, 0, 0, 0.66, 0,
555.67249, 144.32745999999997, 0, 0, 0.66, 0,
485.69398, 97.14663999999999, 0, 0, 0.66, 0,
400, 79.84582, 0, 0, 0.66, 0,
314.30601, 97.14663999999999, 0, 0, 0.66, 0,
244.32752, 144.32745999999997, 0, 0, 0.66, 0,
197.14662, 214.30606999999998, 0, 0, 0.66, 0,
179.84583, 300.00001, 0, 0, 0.66, 0,
197.14662, 385.69395, 0, 0, 0.66, 0,
244.32752, 455.67251, 0, 0, 0.66, 0,
314.30601, 502.853335, 0, 0, 0.66, 0,
400, 520.154145, 0, 0, 0.66, 0,
485.69398, 502.853335, 0, 0, 0.66, 0,
555.67249, 455.67251, 0, 0, 0.66, 0,
602.85338, 385.69395, 0, 0, 0.66, 0
}
},
{
{
399.96981, 520.154415, 0, 0.66, 0.87, 0.53,
314.31022, 502.84844499999997, 0, 0.66, 0.87, 0.53,
244.33872000000002, 455.66152, 0, 0.66, 0.87, 0.53,
197.15180000000004, 385.69002, 0, 0.66, 0.87, 0.53,
179.84583000000003, 300.03043, 0, 0.66, 0.87, 0.53,
197.15180000000004, 214.36131, 0, 0.66, 0.87, 0.53,
244.33872000000002, 144.36892, 0, 0.66, 0.87, 0.53,
314.31022, 97.16106000000002, 0, 0.66, 0.87, 0.53,
399.96981, 79.84559000000002, 0, 0.66, 0.87, 0.53,
357.14002, 88.49858, 0, 0.66, 0.87, 0.53,
322.15427, 112.09205000000003, 0, 0.66, 0.87, 0.53,
298.5608, 147.07779000000005, 0, 0.66, 0.87, 0.53,
289.90781999999996, 189.90759000000003, 0, 0.66, 0.87, 0.53,
298.5608, 232.74691, 0, 0.66, 0.87, 0.53,
322.15427, 267.75356, 0, 0.66, 0.87, 0.53,
357.14002, 291.36794, 0, 0.66, 0.87, 0.53,
399.96981, 300.03042999999997, 0, 0.66, 0.87, 0.53,
442.79961, 308.68341, 0, 0.66, 0.87, 0.53,
477.78535, 332.27689, 0, 0.66, 0.87, 0.53,
501.37883, 367.26262999999994, 0, 0.66, 0.87, 0.53,
510.03181, 410.09241999999995, 0, 0.66, 0.87, 0.53,
501.37883, 452.92222, 0, 0.66, 0.87, 0.53,
477.78535, 487.90797999999995, 0, 0.66, 0.87, 0.53,
442.79961, 511.501435, 0, 0.66, 0.87, 0.53
},
{
442.79961, 435.81479, 0, 0.66, 0.87, 0.53,
467.13788, 425.74728, 0, 0.66, 0.87, 0.53,
477.23582, 401.43944, 0, 0.66, 0.87, 0.53,
467.13788, 377.10117, 0, 0.66, 0.87, 0.53,
442.79961, 367.00324, 0, 0.66, 0.87, 0.53,
418.49177, 377.10117, 0, 0.66, 0.87, 0.53,
408.42425, 401.43944, 0, 0.66, 0.87, 0.53,
418.49177, 425.74728, 0, 0.66, 0.87, 0.53
},
{
418.49177, 205.62329999999997, 0, 0.66, 0.87, 0.53,
394.18129999999996, 195.52799999999996, 0, 0.66, 0.87, 0.53,
384.11641, 171.1871, 0, 0.66, 0.87, 0.53,
394.18129999999996, 146.87662999999998, 0, 0.66, 0.87, 0.53,
418.49177, 136.81174, 0, 0.66, 0.87, 0.53,
442.83266999999995, 146.87662999999998, 0, 0.66, 0.87, 0.53,
452.92796999999996, 171.1871, 0, 0.66, 0.87, 0.53,
442.83266999999995, 195.52799999999996, 0, 0.66, 0.87, 0.53
}
}
};
final List<Double> allTriangles = new ArrayList<>();
GLUtessellator tessellator = gluNewTess();
GLUtessellatorCallback callback = new GLUtessellatorCallbackAdapter() {
int type;
List<Double> vertices = new ArrayList<>();
@Override
public void begin(int type) {
this.type = type;
vertices.clear();
}
@Override
public void end() {
switch (type) {
case GL_TRIANGLES:
break;
case GL_TRIANGLE_FAN:
this.vertices = fanToTriangles(vertices);
break;
case GL_TRIANGLE_STRIP:
this.vertices = stripToTriangles(vertices);
break;
}
allTriangles.addAll(vertices);
}
@Override
public void vertex(Object data) {
double[] vertexData = (double[]) data;
for (double d : vertexData) vertices.add(d);
}
@Override
public void combine(double[] coords, Object[] data, float[] weight, Object[] outData) {
double[] combined = {coords[0], coords[1], coords[2], 0, 0, 0};
for (int i = 0; i < data.length; i++) {
double[] vertex = (double[]) data[i];
combined[3] += weight[i] * vertex[3];
combined[4] += weight[i] * vertex[4];
combined[5] += weight[i] * vertex[5];
}
outData[0] = combined;
}
public List<Double> stripToTriangles(List<Double> strip) {
List<Double> triangles = new ArrayList<>();
for (int i = 0; i < strip.size() - 12; i += 6) {
triangles.addAll(strip.subList(i, i + 18));
}
return triangles;
}
public List<Double> fanToTriangles(List<Double> fan) {
List<Double> centralVertex = fan.subList(0, 6),
triangles = new ArrayList<>();
for (int i = 6; i < fan.size() - 6; i += 6) {
triangles.addAll(centralVertex);
triangles.addAll(fan.subList(i, i + 12));
}
return triangles;
}
};
tessellator.gluTessCallback(GLU_TESS_BEGIN, callback);
tessellator.gluTessCallback(GLU_TESS_END, callback);
tessellator.gluTessCallback(GLU_TESS_VERTEX, callback);
tessellator.gluTessCallback(GLU_TESS_COMBINE, callback);
for (double[][] polygon : complicatedShape) {
tessellator.gluTessBeginPolygon(null);
for (double[] contour : polygon) {
tessellator.gluTessBeginContour();
for (int i = 0; i < contour.length - 5; i += 6) {
double[] vertexData = {
contour[i], contour[i + 1], contour[i + 2],
contour[i + 3], contour[i + 4], contour[i + 5]
};
tessellator.gluTessVertex(vertexData, 0, vertexData);
}
tessellator.gluTessEndContour();
}
tessellator.gluTessEndPolygon();
}
FloatBuffer vertices = BufferUtils.createFloatBuffer(allTriangles.size());
for (double d : allTriangles) vertices.put((float) d);
vertices.flip();
int verticeHandle = glGenBuffers();
glBindBuffer(GL_ARRAY_BUFFER, verticeHandle);
glBufferData(GL_ARRAY_BUFFER, vertices, GL_STATIC_DRAW);
glVertexPointer(3, GL_FLOAT, 6 << 2, 0);
glColorPointer(3, GL_FLOAT, 6 << 2, 3 << 2);
glEnableClientState(GL_VERTEX_ARRAY);
glEnableClientState(GL_COLOR_ARRAY);
while (!Display.isCloseRequested()) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glDrawArrays(GL_TRIANGLES, 0, allTriangles.size() / 6);
Display.update();
Display.sync(60);
}
glDisableClientState(GL_COLOR_ARRAY);
glDisableClientState(GL_VERTEX_ARRAY);
}
}